夕陽下,鳥兒成群舞動,時而疏散,時而聚攏,不斷變化著空間排序卻能互不相撞,既能飛越障礙也不會彼此失散。鳥群如何在空中舞蹈、魚群如何在水中變幻?
2021年,一艘貨輪意外在蘇伊士運河擱淺,給全球經濟帶來“多米諾骨牌”式影響,每天由此減少的貿易額高達90億美元,為什么小小一艘貨輪能堵住全球供應鏈?同樣地,為什么一條網絡謠言可以引爆全網大規模輿情?難道一只蝴蝶輕輕振翅,真能卷起千里之外的一場風暴嗎?
這些問題看似毫不相關,但仔細思考就會發現,這些復雜現象均有一個共同點:它們都發生在由大量主體通過相互作用構成的復雜系統中。2021年諾貝爾物理學獎頒發給了意大利物理學家喬治·帕里西教授(Giorgio Parisi)以表彰他對復雜系統理論的開創性貢獻。年輕時的喬治·帕里西教授也曾在羅馬火車站,對空中成千上萬只鳥兒成群飛翔的景象著迷。他常佇立良久,觀察、拍攝鳥群。基于對鳥群的觀察數據,帕里西教授用統計物理方法揭開了鳥群飛行的奧秘[1]。原來每只鳥只需要遵循三個最基本的原則,就可以復現鳥群飛翔的奇景。這三個基本原則為:(1)靠近視野中的鄰居,每只鳥都希望與視野中的同伴攜行;(2)與視野中的鄰居保持一致的飛行方向;(3)當與鄰居過于靠近時,調整方向,避免碰撞。
所以,鳥群飛行的奧秘不在于每只鳥,而是它們之間的相互作用。鳥群飛行如此復雜,但背后規則竟如此簡單!研究鳥群這樣的系統時出現一個魔咒:我們慣于依賴的還原論失效了。
還原論雖然不能理解鳥群的集體行為,但對理解飛機就很有效,盡管飛機的零件也不計其數,功能也眼花繚亂,但只要我們明白每個零件的作用,就能完全理解飛機的飛行原理。我們稱飛機這樣的系統為復合系統(Complexed systems),而像鳥群、大腦這樣的系統,即使我們研究清楚了系統的所有組成部分(如每只鳥、每個神經元),也無法理解系統整體涌現的奇觀(如鳥群飛舞、意識涌現),這樣的系統就是復雜系統(Complex systems),如圖1所示。復雜系統研究旨在解決的核心問題就是探索復雜系統背后的簡單、普適規律。

圖1 復合系統與復雜系統
牛頓建立了機械性、確定性的物理王國。像小球從斜面滑下的故事時刻都被牛頓力學牢牢控制。在這個確定性王國里,只要我們給定了系統的初始狀態,那萬物都將按照確定的規則運行。1961年的冬天,氣象學家洛倫茨(Edward Norton Lorenz)構建了一個精巧的數學模型,希望能預測天氣,卻意外地發現了另一個世界。計算機千分之二的系統誤差(0.0001秒)竟會得到截然不同的結果。所謂“差之毫厘,謬以千里”。他把這個高度非線性的天氣模型輸入到計算機中,得到的狀態軌跡竟像一只張開翅膀的蝴蝶。于是就有了大家非常熟悉的蝴蝶效應(如圖2所示),這一效應形象地表現了非線性系統對初值的敏感性,也體現了復雜系統一個有趣的現象——混沌。
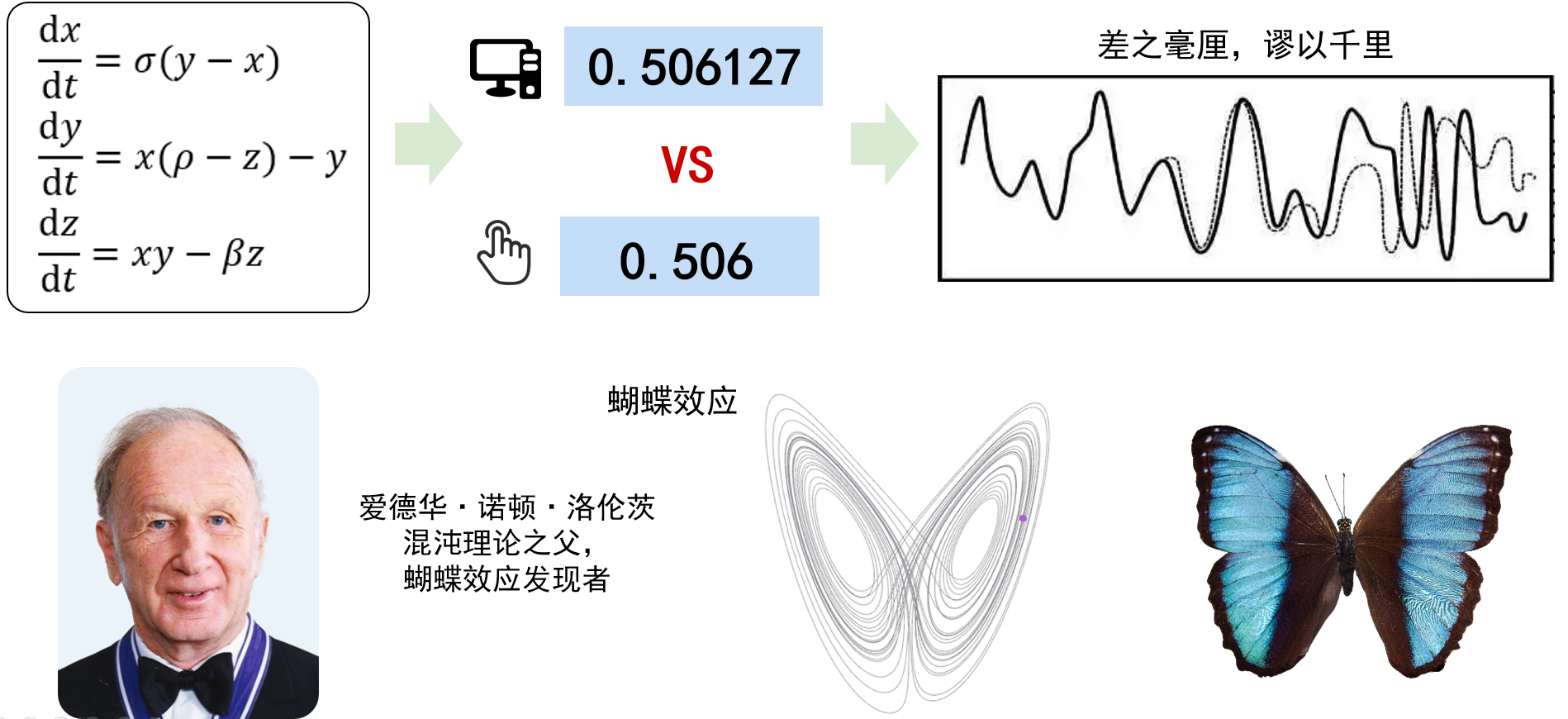
圖2 蝴蝶效應起源
實際上,大多數我們熟悉的真實系統,既不是混沌的,也不是完全秩序的,而是處于兩者之間,我們稱之為混沌與秩序的邊緣狀態。復雜性科學正是誕生于混沌與秩序邊緣的科學。1984年,在蓋爾曼、安德遜和阿羅等人的支持下,一批從事物理、經濟和計算機領域的科學家在圣塔菲伊蘇區中一個租來的女修道院中組建了圣達菲研究所(Santa Fe Institute)。該研究所如今已經成為世界知名的復雜科學研究中心。以圣塔菲研究所成員為代表的一大批學者,嘗試突破牛頓以來的還原論思維桎梏,理解涌現、混沌等復雜系統現象。
圣塔菲研究所的創始人之一喬治·考溫曾說,他們正在開創二十一世紀的科學。如今,未來已來!經過科學家們三十多年來的努力,如今復雜科學又迎來了一個新發展階段——應用復雜網絡來刻畫、研究復雜系統。網絡科學應運而生。網絡科學的核心思路,就是應用復雜網絡對各類復雜系統進行建模[2]。在現實世界中,大到全球生態系統和全球物流系統,小到細胞內的蛋白質交互系統,都可以用復雜網絡進行建模(如圖3所示),其中節點表示系統的組成元素,連邊表示元素之間的相互作用,通過研究系統抽象而成的網絡結構及其上的動力學,就可以理解網絡所對應的復雜系統的規律。
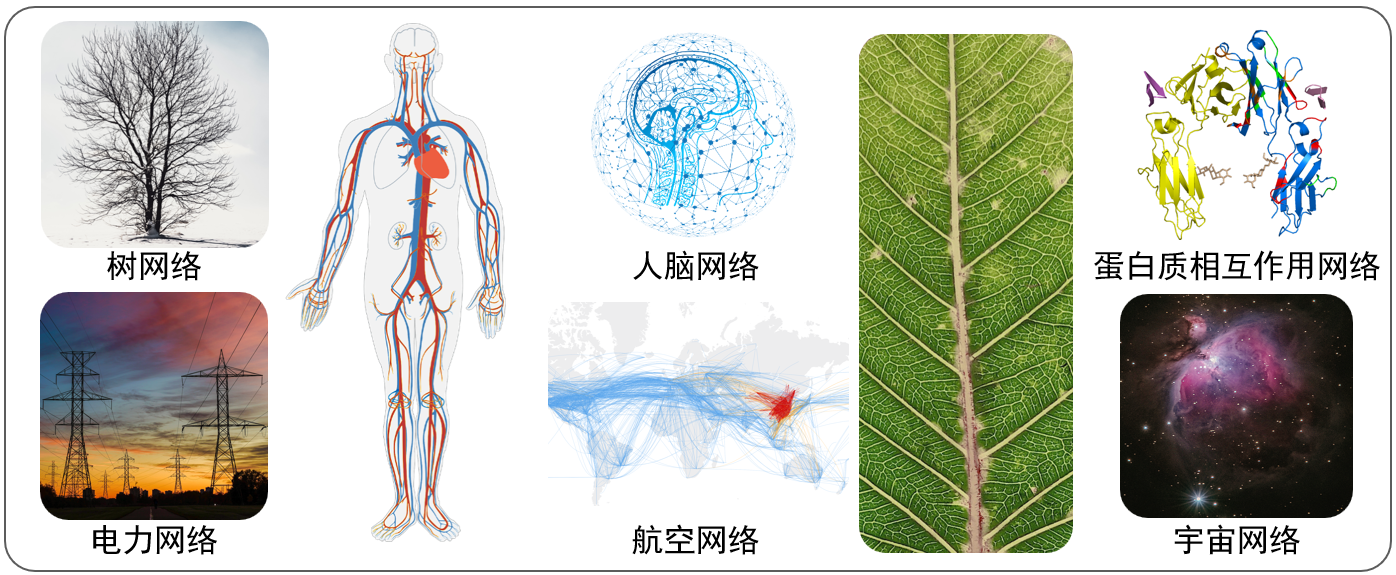
圖3 多種復雜網絡實例
社交網絡是我們日常生活中最為熟悉的網絡,每個人作為社交網絡中的節點,通過線上線下關系聯系起來。回到剛開始的問題,為什么一條網絡謠言可以引爆全網大規模輿情,我們又應該從何入手、控制輿情呢?解決這些問題的關鍵在于在社交平臺上找到謠言傳播過程中的關鍵人物,以及識別和切斷重要的傳播路徑。歸結起來就是對兩個關鍵科學問題的探索:如何挖掘網絡中的重要節點[3],以及如何挖掘網絡中的重要鏈路[4]。這兩個問題的研究在網絡科學中被稱為網絡信息挖掘(如圖4所示)。
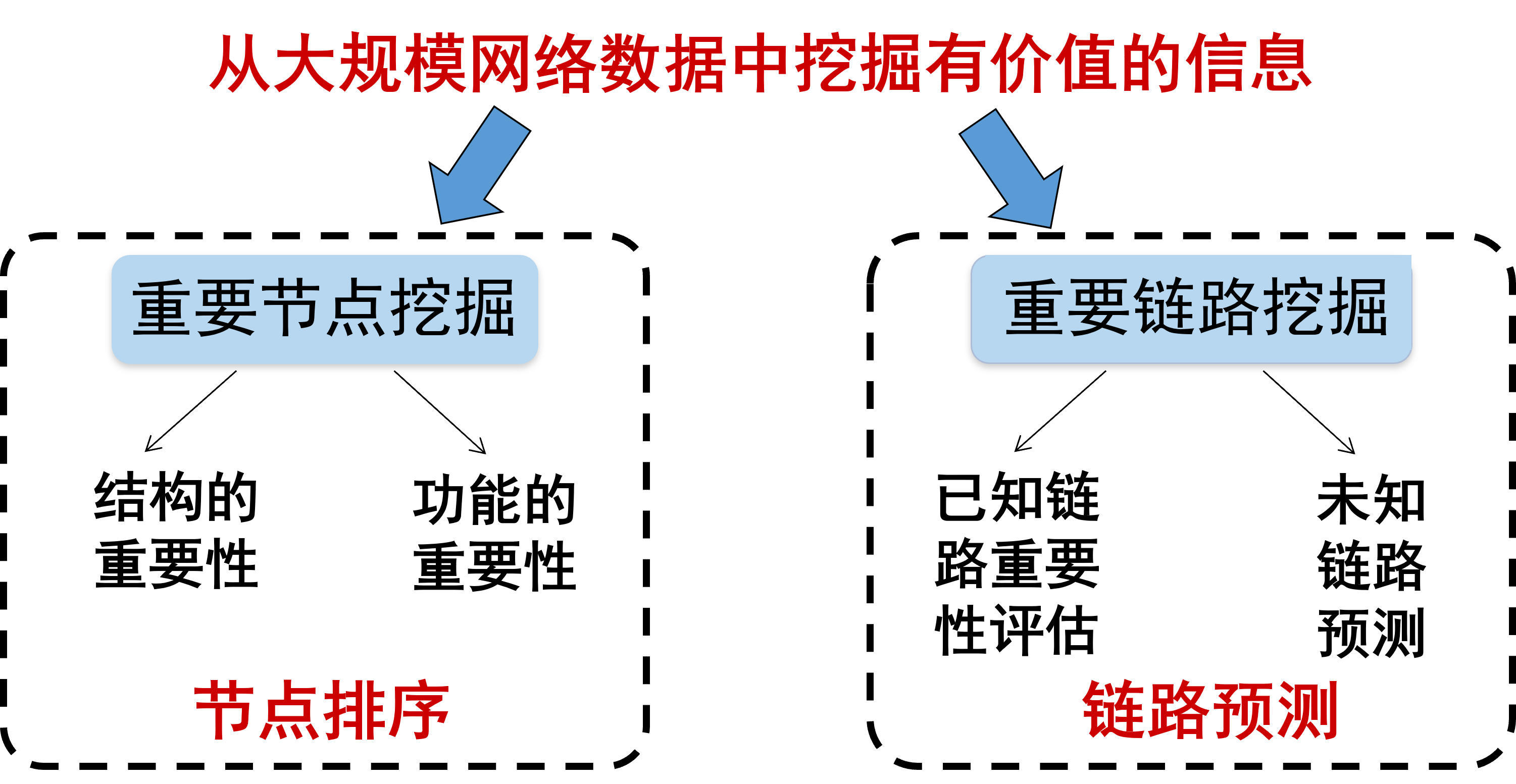
圖4 網絡信息挖掘
對于第一個科學問題:如何基于已知的網絡信息挖掘出對網絡結構和功能產生重要影響的節點,其實是如何對節點進行排序的問題。在解決這一問題的方法中,依據節點的核數進行排序是一種經典的方法(即K-core分解[5]),它刻畫了節點在網絡中的位置。這就像一個剝洋蔥的過程,把網絡一層一層剝掉,越晚剝掉的節點處于網絡中的核心位置,這個節點的影響力也就越大。但這樣的方法大多適用于靜態的、簡單的網絡。而在現實生活中我們面對的網絡大多數都是大規模、含權、演化、有向的。面對這樣的復雜網絡時,我們又該如何快速高效地計算核數,挖掘出重要節點呢?
受到科學家H指數的啟發,我們定義了一個局部H算子[6],將算子H作用在有限的實數序列上,得到y=H(x1,x2,...,xn)。H算子的定義為在實數序列(x1,x2,...,xn),最多找到y個不小于y的數(如圖5所示),這個概念與H指數的概念完全一致。當我們把H算子作用在網絡的節點度序列上時,返回的y值就稱為該節點的一階H指數,將H算子進一步作用在某節點的鄰居的一階H指數上時,可以得到該節點的二階H指數。經過這樣連續的作用,就能得到節點的H指數序列。有趣的是,這個序列可以被嚴格證明為收斂于節點的核數。
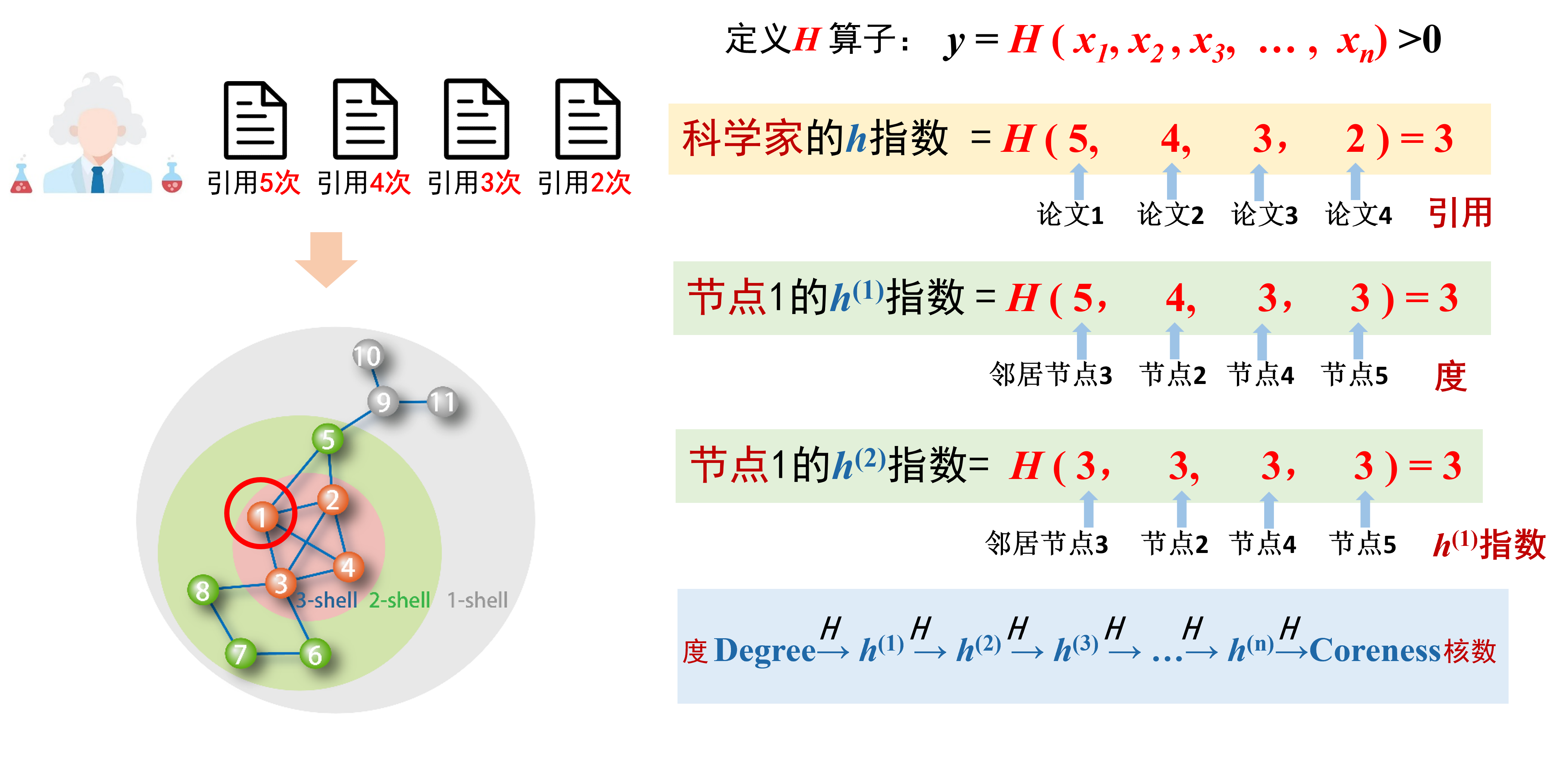
圖5 H算子定義示意圖
因此,通過H算子,我們把長期以來被認為毫不相關的三個指標:度、H-指數與核數聯系了起來,我們稱這一發現為網絡的DHC定理[6](如圖6所示)。這個定理對于演化、含權、有向網絡同樣適用。基于該定理就可以通過分布式的方式僅基于網絡節點局部的信息快速計算節點的核數,從而快速準確地挖掘出復雜網絡中的重要節點。
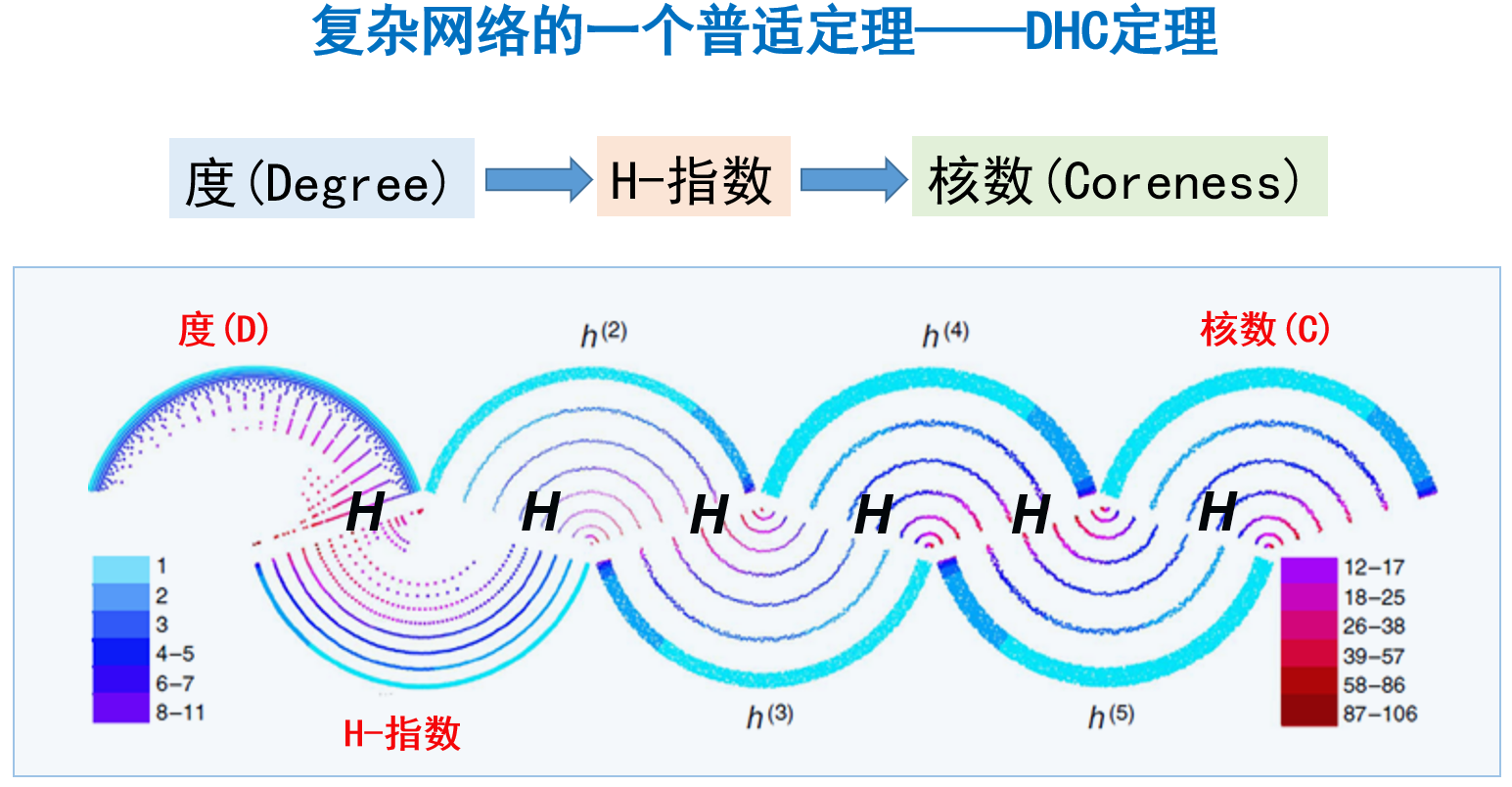
圖6 DHC定理
我們發現,在微博網絡中應用DHC定理去識別關鍵用戶,只需要監測不到四萬分之一的微博用戶就可以跟蹤95%以上的重大食品安全輿情。此外,這一方法還可以應用在國家創新力分析[7]、重要腦區識別[8]、城市媒體影響力分析[9]等多個領域中。
對于第二個科學問題,如何基于已知的網絡結構信息和可能的節點屬性信息,估計兩個未連接節點之間產生連接的可能性?這個問題被稱作鏈路預測,社交網絡中的“好友推薦”就是典型的鏈路預測問題的應用。在鏈路預測研究中,數據和算法直接決定了預測精度。當獲得一個較差的預測結果時,我們就往往會探究怎么設計更好的算法。但卻忽略了一個非常關鍵的問題:分析的數據本身是否是可預測的,即如何刻畫網絡數據的可預測性。
我們認為,如果隨機從網絡中抽取出一小部分鏈路,網絡的特征向量空間受到的影響很小,就說明網絡是具有規律性的,即可預測性高的。在這種思路的基礎上,我們應用類似于量子力學中對哈密頓量做一階微擾的方法,假定減少或者加入少量鏈接所產生的微擾,只對特征值有影響,而對特征向量沒有影響,這樣就可以觀察微擾后通過這種辦法重構的鄰接矩陣和真實鄰接矩陣的差異。我們提出了一個度量這種差異的指標——網絡的結構一致性[10]。一致性越強則表示該網絡的可預測性越大。依據這個思路,我們進一步提出了基于網絡結構微擾的鏈路預測模型(如圖7所示)。這個方法在預測丟失的鏈路以及甄別網絡中添加的噪音邊兩方面都明顯超過了經典的層次結構模型和隨機分塊模型等等。相關算法不僅可以用在社交領域的關系預測中,還可以用在乳腺癌、肺癌、心衰等多種致病基因的預測,預測精度高于傳統的系統生物學方法[11]。

圖 7 網絡結構一致性計算
網絡信息挖掘具有非常廣泛的應用場景。目前已有部分研究成果應用于網絡輿情監控、致病基因預測、醫保欺詐識別、電子商務服務等實際系統中,產生了一定的社會經濟價值。二十大報告中強調了產業鏈供應鏈對于國家安全的重要性,要求著力提升產業鏈供應鏈韌性和安全水平,網絡信息挖掘的相關方法也能應用于相關研究中發揮作用。產業鏈供應鏈天然就是一張網,可以用復雜網絡進行描述刻畫(如圖8所示),其中供應鏈是上下游企業為實現將產品或服務交付給最終用戶而形成的產-銷關系網絡,產業鏈是各產業之間依據一定經濟技術聯系、空間布局形成的相互關聯網絡。通過構建網絡,就可以通過識別重要節點,提前發現可能被“卡脖子”的產業;通過識別重要鏈路,優化重要鏈路及提前預警薄弱環節等,結合從微觀節點到宏觀網絡全局的視角,提出產業鏈供應鏈的優化升級策略,保障產業鏈供應鏈的自主可控和安全高效。
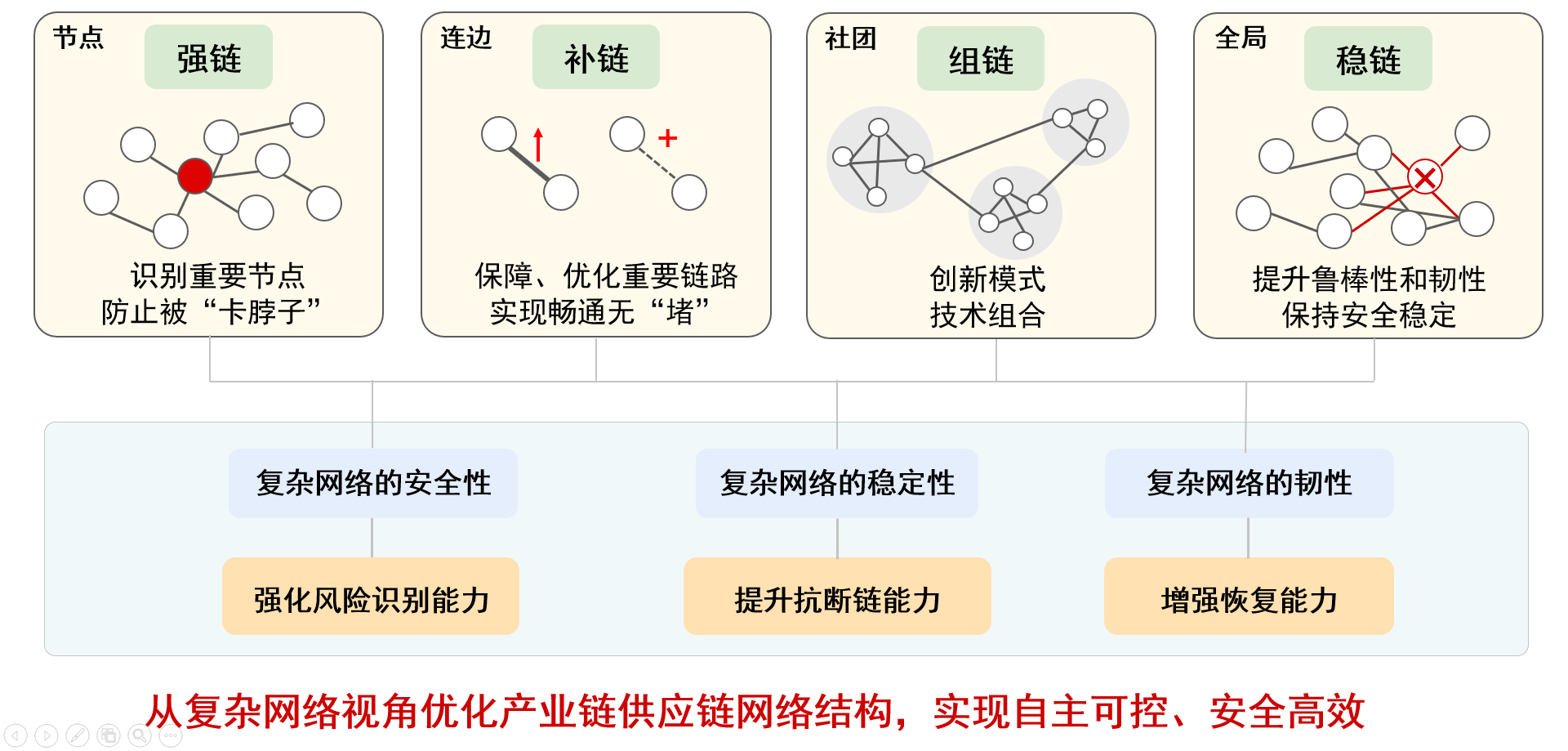
圖 8 復雜網絡視角優化產業鏈供應鏈網絡
圖論作為復雜網絡的重要基石之一,其源頭最早可以追溯到歐拉的哥尼斯堡七橋問題。直到1998年小世界網絡、1999年無標度網絡的突破性進展,掀起了網絡科學過去二十多年的研究熱潮。目前,我們在節點和連邊層面對網絡的結構、動力學、預測和控制有了較成熟的理解。然而隨著研究的不斷深入,研究人員發現很多現實系統中不僅包含節點對之間的二元關系,還包括以群、組的形式發生的高階相互作用[12],比如,一篇學術論文可能是由多名學者共同完成的;生物信號傳遞、基因表達調節等生命過程需要多種蛋白質的參與;在大腦神經網絡中,包括記憶在內的很多認知功能,都依賴于神經元群的編碼和信號同步。這種高階相互作用難以用基于二元交互關系的網絡進行很好地描述。當我們回溯網絡科學的起源時,會有一些新的思路(如圖9所示)。我們發現,歐拉另外一個重要貢獻——歐拉示性數以及龐加萊的洞公式等研究為網絡科學提供了新的思路,可以用來研究多節點相互作用的高階結構和動力學問題,從而將網絡科學的研究推進到高階網絡分析的時代。高階網絡分析使我們可以獲得對網絡的結構和功能更深刻的洞見,并有望在一些已有難題上突破瓶頸、獲得新發現。
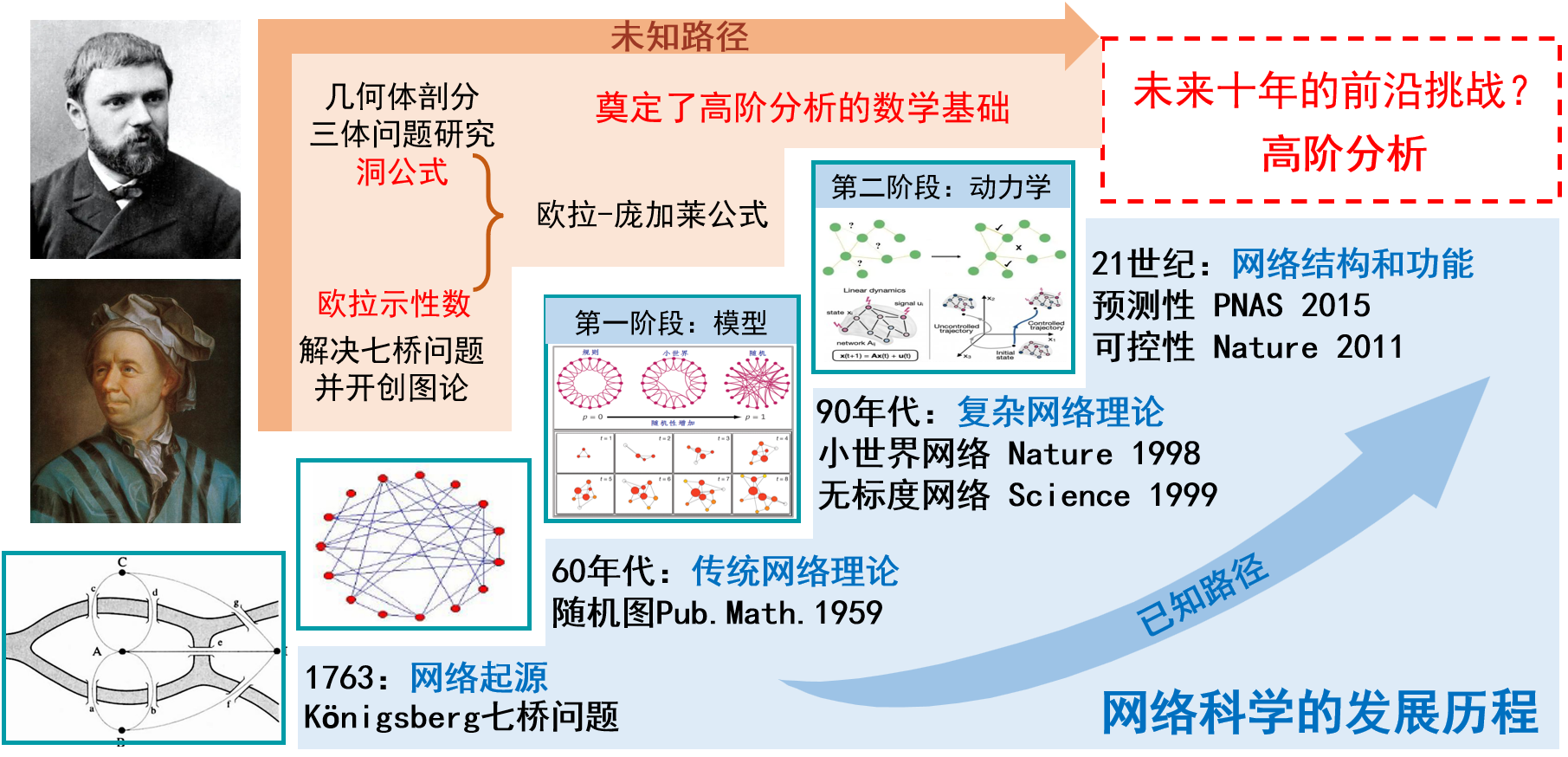
圖 9 網絡科學發展歷程及未來前沿挑戰
從社會過程到神經科學的眾多復雜系統實例上,高階拓撲分析都展示出了巨大潛力。網絡高階結構中,最基本的就是圈結構,包括團和洞(如圖10所示)。而人腦中團和洞,前者作為信息處理和記憶的單元,后者作為跨腦區信息整合和分發的功能基礎,對于人腦的并行處理與高級認知活動至關重要[13]。進行網絡高階拓撲分析的首要任務是要找到網絡中的高階結構。但目前為止,關于網絡高階結構的研究還沒有形成系統的理論方法。比如繪制大腦完整的高階結構圖譜現在仍是一個巨大的挑戰。
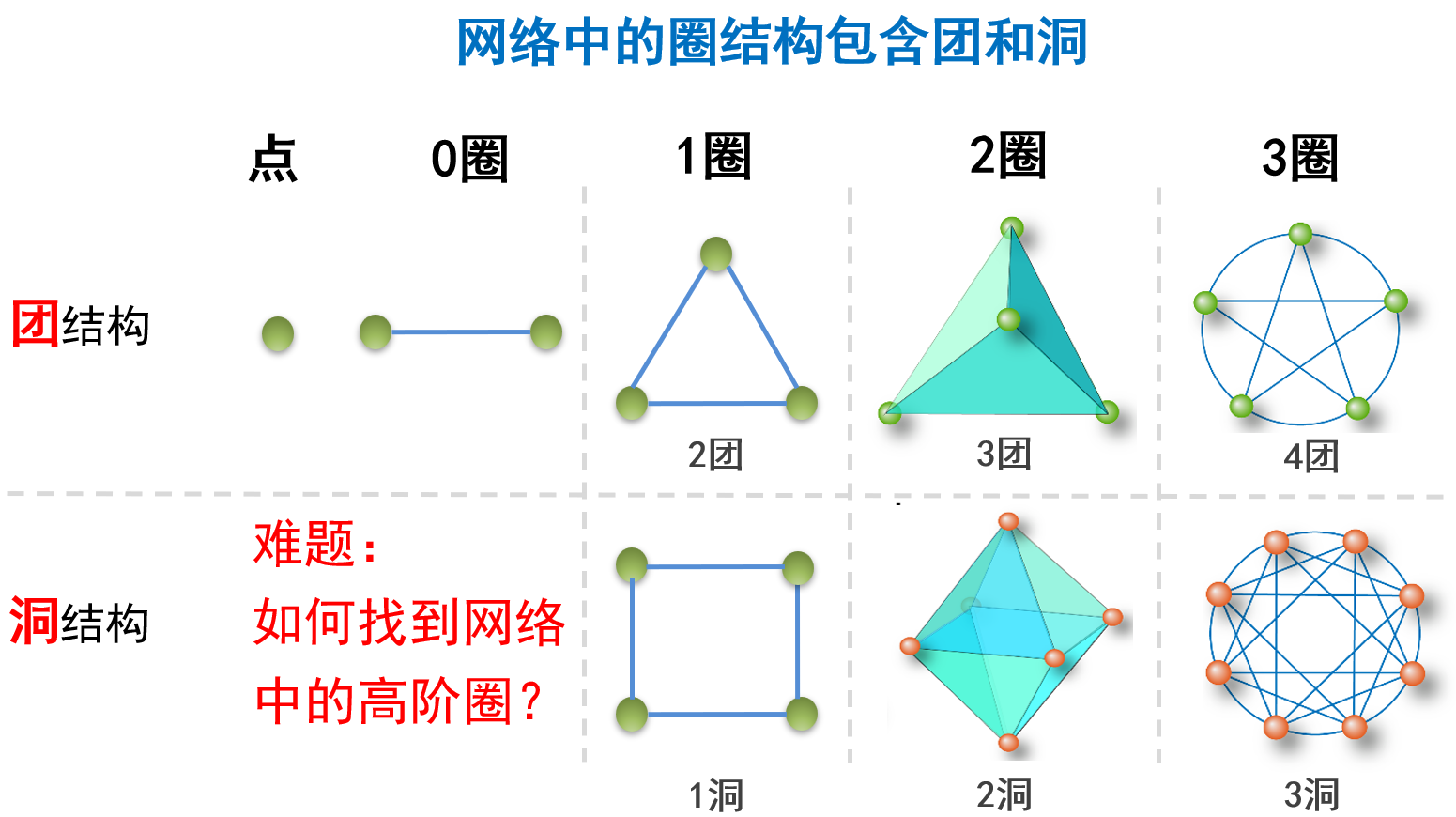
圖10 團、洞結構示意圖
尋找網絡高階結構的關鍵在于,如何計算網絡結構。我們借鑒龐加萊對幾何體剖分的思想,把網絡看成一個幾何體,然后對它進行類似的剖分,分解成全齊性子網絡[14]。然后再采用一些二元域上的向量空間和邊界算子對網絡進行描述和計算。基于此,我們就可以計算出網絡中的團、洞結構,以及拓撲不變量,最后呼應歐拉-龐加萊公式,進一步驗證計算的準確度(如圖11所示)。我們將這套方法應用在線蟲的神經網絡中,計算出線蟲神經網絡全部團、洞的數目,繪制了線蟲神經網絡完整的高階結構圖譜[15]。而這些團、洞結構的生物學意義還有待進一步解讀。
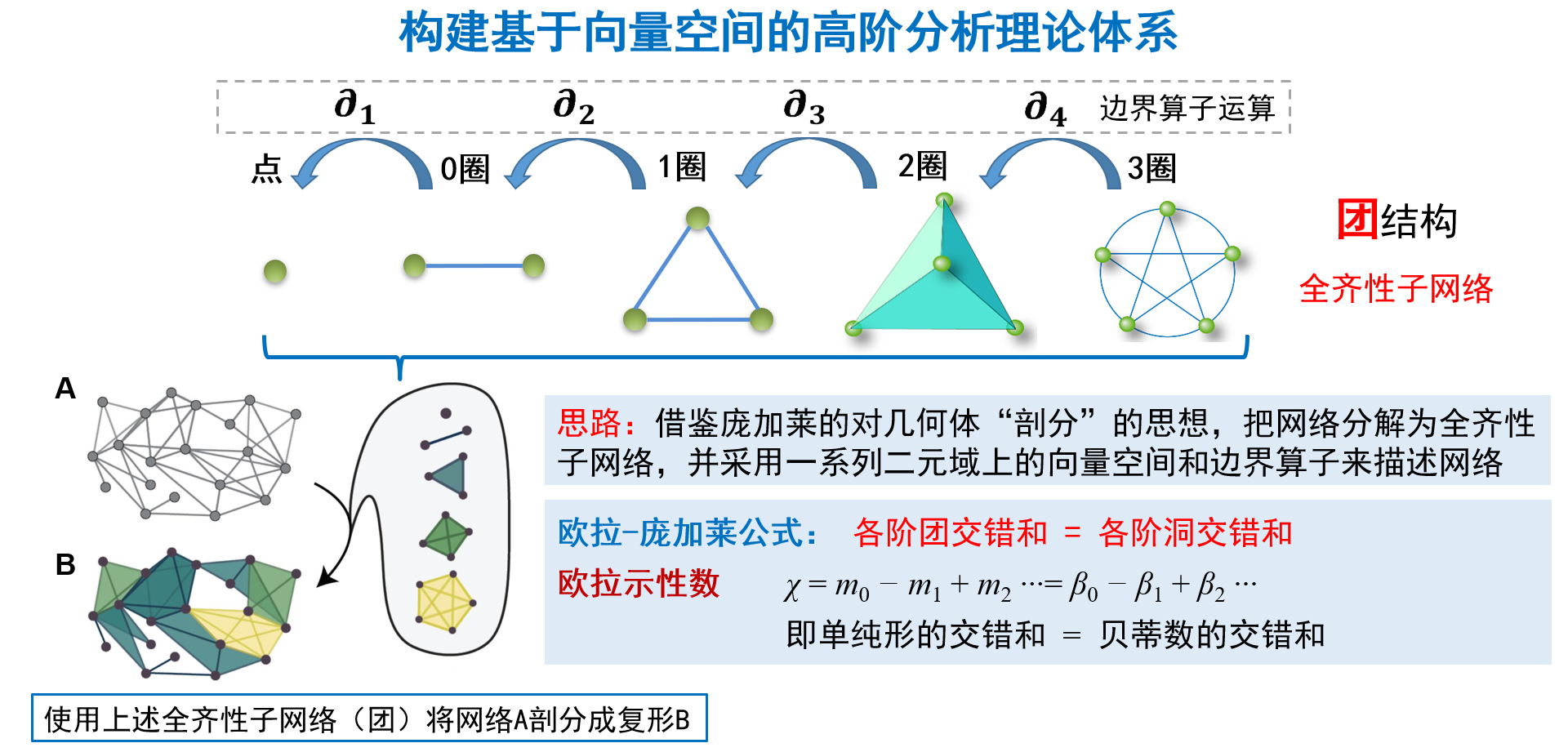
圖11 高階網絡分析理論框架
應用高階網絡分析來理解大腦會是一個全新的視角。團、洞等高階結構在大腦中非常關鍵,這也將促進我們對腦功能相關的神經環路的理解和認識,為臨床應用和開發類腦計算框架提供了新思路。比如,我們對孤獨癥患者大腦神經網絡的分析顯示,與健康人相比,孤獨癥患者腦網絡中的“團少洞多”。團在一定程度上反映了局部并行處理信息的能力,洞反映了大腦對不同腦區信息整合的能力。這就說明孤獨癥患者局部并行處理信息的能力有所降低,但是跨腦區信息整合的能力得到提升。但是具體而言,這些團、洞結構如何以特定的組織方式形成,它們與認知和疾病之間究竟有何關聯?這都是未來需要進一步研究的重要問題。
在未來,網絡科學與人工智能的結合將有著巨大潛力。它不僅有望解決當前的挑戰,比如說現代數字化社會的安全和治理問題,同時也將催生一些新的科學問題和應用技術,在社會、經濟等眾多領域發揮重要作用(如圖12所示)。從1984年圣塔菲研究所成立、復雜性科學誕生,到2021年諾貝爾物理學獎授予復雜系統研究,復雜科學在短短幾十年里迅速成長,但它仍然像一個青春期的孩子,既稚嫩又代表著未來。復雜科學方興未艾,中國學者未來可期!

圖12 網絡科學與人工智能結合的應用場景
參考文獻
[1] 喬治·帕里西. 隨椋鳥飛行. 文錚, 譯. 2022.
[2] NEWMAN M E J. The structure and function of complex network. SIAM Review, 2003, 45(2): 167-256.
[3] Lü, L., Chen, D., Ren, X. L., Zhang, Q. M., Zhang, Y. C., & Zhou, T. Vital nodes identification in complex networks. Physics Reports 650, 1–63 (2016).
[4] 呂琳瑗, 周濤. 鏈路預測. 高等教育出版社, 2013[2023-08-12].
[5] Alvarez-Hamelin, J. I., Dall’Asta, L., Barrat, A. & Vespignani, A. k-core decomposition: a tool for the visualization of large scale networks. Preprint at https://doi.org/10.48550/arXiv.cs/0504107 (2005).
[6] Lü, L., Zhou, T., Zhang, Q.-M. & Stanley, H. E. The H-index of a network node and its relation to degree and coreness. Nature Communications 7, 10168 (2016).
[7] Ye, Y., Xu, S., Mariani, M. S. & Lü, L. Forecasting countries’ gross domestic product from patent data. Chaos, Solitons & Fractals 160, 112234 (2022).
[8] Wang, H., Wu, H.-J., Liu, Y.-Y. & Lü, L. Higher-order interaction of brain microstructural and functional connectome. Preprint at https://www.biorxiv.org/content/10.1101/2021.11.11.467196v1.abstract (2021).
[9] 范天龍, 朱燕燕, 吳蕾蕾, 等. DHC定理在有向含權網絡上的推廣及應用 電子科技大學學報, 2017, 46(5): 766-776.
[10] Lü, L., Pan, L., Zhou, T., Zhang, Y.-C. & Stanley, H. E. Toward link predictability of complex networks. Proceedings of the National Academy of Sciences 112, 2325–2330 (2015).
[11] Zeng, X., Liu, L., Lü, L. & Zou, Q. Prediction of potential disease-associated microRNAs using structural perturbation method. Bioinformatics 34, 2425–2432 (2018).
[12] Boccaletti, S., De Lellis, P., del Genio, C. I., Alfaro-Bittner, K., Criado, R., Jalan, S., & Romance, M. The structure and dynamics of networks with higher order interactions. Physics Reports, 1018, 1-64 (2023).
[13] Sizemore, A. E., Giusti, C., Kahn, A., Vettel, J. M., Betzel, R. F., & Bassett, D. S. Cliques and cavities in the human connectome. Journal of Computational Neuroscience, 44, 115-145 (2018).
[14] Shi, D., Lü, L. & Chen, G. Totally homogeneous networks. National Science Review 6, 962–969 (2019).
[15] Liu, B., Yang, R., Wang, H. & Lü, L. Complete cavity map of the C. elegans connectome. Preprint at http://arxiv.org/abs/2212.03660 (2022).